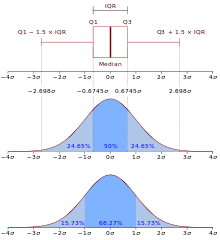
四分位距
四分位距（英语：interquartile range, IQR）。是描述统计学中的一种方法，以确定第三四分位数和第一四分位数的分别（即
Q
1
,
Q
3
{displaystyle Q_{1}, Q_{3}}
的差距）[1]。与方差、标准差一样，表示统计资料中各变量分散情形，但四分差更多为一种稳健统计（robust statistic）。
四分位差（英语：Quartile Deviation, QD），是
Q
1
,
Q
3
{displaystyle Q_{1},Q_{3}}
的值差的一半，即
Q
D
=
Q
3
−
Q
1
2
{displaystyle mathrm {QD} ={frac {Q_{3}-Q_{1}}{2}}}
。
定义
四分位距通常是用来构建箱形图，以及对概率分布的简要图表概述。对一个对称性分布数据（其中位数必然等于第三四分位数与第一四分位数的算术平均数），二分之一的四分差等于绝对中位差（MAD）。中位数是聚中趋势的反映[2]。
I
Q
R
=
Q
3
−
Q
1
{displaystyle mathrm {IQR} =Q_{3}-Q_{1}}
举例
图表中的数据
数列
参数
四分差
1
102
2
104
3
105
Q
1
{displaystyle Q_{1}}
4
107
5
108
6
109
Q
2
{displaystyle Q_{2}}
（中位数）
7
110
8
112
9
115
Q
3
{displaystyle Q_{3}}
10
118
11
118
从这个图示中，我们可以算出四分差的距离为
115
−
105
=
10
{displaystyle 115-105=10}
。
箱形图中的数据
—– –
o * |——-| | |—|
—– –
— — — — — — — — — — — — 数列
0 1 2 3 4 5 6 7 8 9 10 11 12
从该图中我们可算出:
第一四分位数
(
Q
1
,
x
0.25
)
=
7
{displaystyle (Q_{1},x_{0.25})=7}
中位数（第二四分位数）
(
M
e
d
,
x
0.5
)
=
8.5
{displaystyle (mathrm {Med} ,x_{0.5})=8.5}
第三四分位数
(
Q
3
,
x
0.75
)
=
9
{displaystyle (Q_{3},x_{0.75})=9}
四分位距
I
Q
R
=
Q
3
−
Q
1
=
2
{displaystyle mathrm {IQR} =Q_{3}-Q_{1}=2}
四分位差
Q
D
=
Q
3
−
Q
1
2
=
1
{displaystyle mathrm {QD} ={frac {Q_{3}-Q_{1}}{2}}=1}
相关条目
参考文献
^ What is an interquartile range?. [2009-09-18]. （原始内容存档于2009-09-25）.
外部链接
Interquartile Range（页面存档备份，存于互联网档案馆）
QuartileDeviation（页面存档备份，存于互联网档案馆）
